本文主要就二叉树的遍历方式进行总结和记录,从而了解递归、栈以及队列的应用,通常对于一个二叉树的遍历方式大致分为:
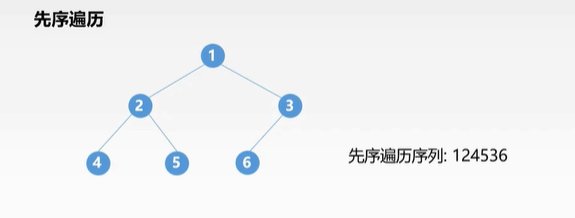
- 前序遍历(中 -> 左 -> 右)
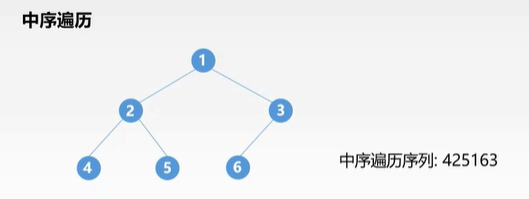
- 中序遍历(左 -> 中 -> 右)
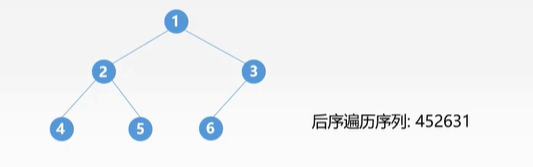
- 后续遍历(左 -> 右 -> 中)
- 层次遍历
栈实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23/*
* 思路:若二叉树非空
* 1、根遍历,拿到一个节点的指针,先判断是否为空,不为空就先访问该结点,然后直接进栈,
* 2、接着遍历左子树;为空则要从栈中弹出一个节点来,这个时候弹出的结点就是其父亲
* 3、然后访问其父亲的右子树,直到当前节点为空且栈为空时,算法结束.
*
*/
public void PreOrder1(Btree T) {
stack<Btree> st;
if (T == NULL){
return null;
}
st.push(T);
while (!st.empty()){
Btree T =st.pop();
show(T)
if (T.right!=NULL)
st.push(p.right);
if (p.left!=NULL)
st.push(p.left);
}
return null;
}
栈实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22/*
* 思路:借助栈
* 1、初始时依次扫描根节点的所在左侧节点并将它们一一进栈;
* 2、出栈一个节点,访问它
* 3、扫描该节点的右孩子节点并将其出栈
* 4、依次扫描右孩子节点的所有左侧节点并一一进栈
* 5、反复 2 - 4 步骤
*/
public void MidOrder2(Btree T){
Stack s = new Stack();
BTree p = T;
while(p||!s.IsEmpty()){
if(p){
s.push(p);
p = p.left;
}else{
p = s.pop();
show(p);
p = p.right;
}
}
}
栈实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32/*
* 思路:借助栈
*/
public void AfterOrder2(Btree root){
if (root == NULL){
return;
}
Stack<BTree> s = new Stack();
s.push(root);//根指针入栈
while (!s.empty())
{
//重复将栈顶指针指向结点的左子树压栈,直到栈顶指针指向结点的左子树为空
while (s.top().left != NULL){
s.push(s.top().left);
}
Btree last = NULL;//上一次遍历过的指针
//重复检查
while (!s.empty()){
if (s.top().right==NULL||last==s.top().right) {
//如果栈顶指针指向结点的右子树为空或者遍历过
show(s.top())
last = s.top();//更新指针last
s.pop();//栈顶指针出栈
}
//如果栈顶指针指向的结点的右子树不为空
else if(s.top()->R!=NULL){
s.push(s.top()->R);//将右子树入栈
break;//退出检查
}
}
}
}
队列实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24/*
* 思路:借助队列 队列的就是FIFO
* 1、初始将根节点入队并访问根节点,然后出队
* 2、如果有左子树,将左子树的根入队
* 3、如果有右子树,将右子树的根入队
* 4、然后出队,访问该节点
* 5、反复出队访问直到队列为空
* 伪代码
*/
public void levelOrder(Btree T){
InitQueue(Q)
BTree p;
EnQueue(Q,T)
while(!IsEmpty(Q)){
Dequeue(Q,p);
show(p);
if(p.left != null){
EnQueue(Q,p.left);
}
if(p.right != null){
Enqueue(Q,p.right);
}
}
}